3. Substring Search
Let’s make a leap, since brute force implementation is not consideration because its running time (~NM), our attention here is more efficient algorithms.
Knuth-Morris-Pratt (KMP) Substring Search
The idea of KMP algorithm is by remove backup lookup in brute force algorithm, we can implement substring search in linear time, equal to N characters. For example, we need to find pattern ABABC in text ABABABC. When there is a mismatch in position 4, KMP will choose better restart position which is 2 to continue the search. To make it happen, KMP need to do preprocessing which has running time equal to M. One of proper preprocessing for KMP is DFA (Deterministic Finite Automata).
The graphical implementation of constructing DFA of pattern ABABC illustrate in image 8 and 9.
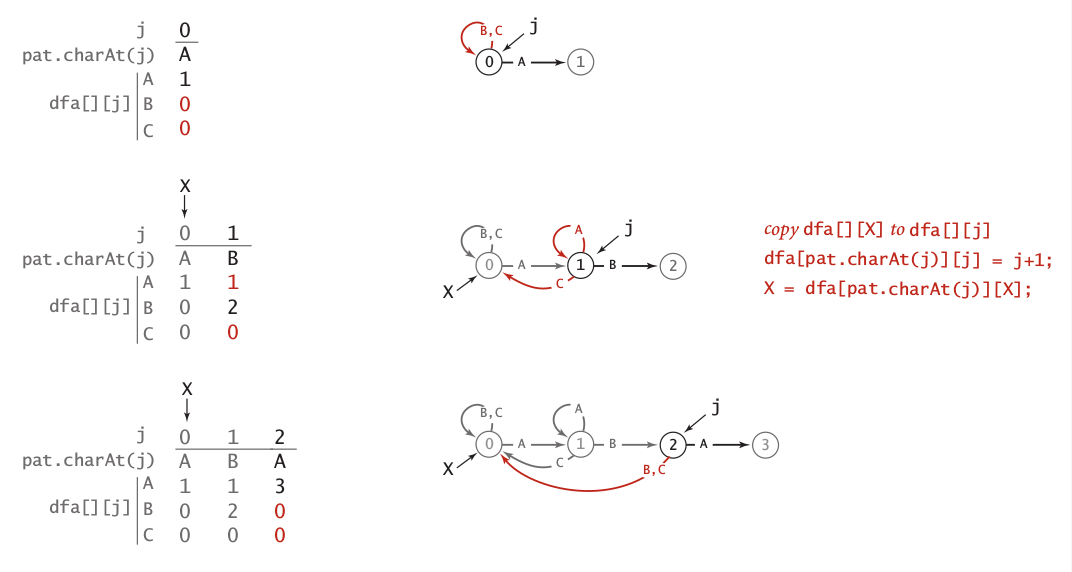Image 8: Constraction of DFA ABABC (1)
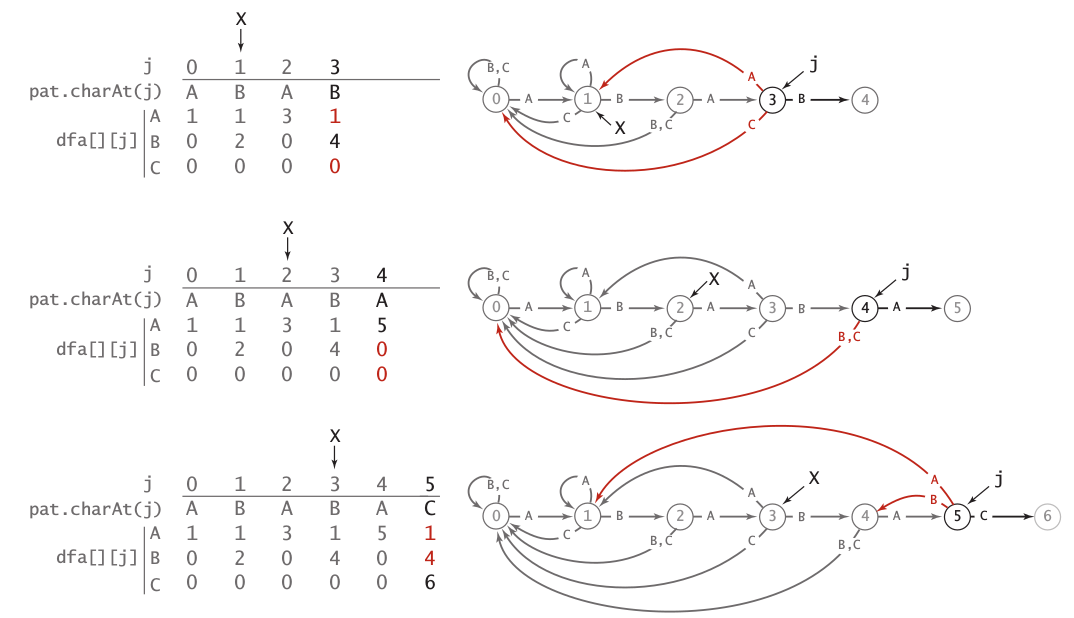Image 9: Construction of DFA ABABC (2)
The implementation of KMP algorithm in java will be like this:
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class KMP
{
private String pat;
private int[][] dfa;
public KMP(String pat)
{ // Construct DFA from pattern
this.pat = pat;
int M = pat.length();
int R = 256;
dfa = new int[R][M];
dfa[pat.charAt(0)][0] = 1;
for (int X = 0, j = 1; j < M; j++) {
// Compute dfa[][]
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][X];
dfa[pat.charAt(j)][j] = j+1;
X = dfa[pat.charAt(j)][X];
}
}
public int search(String txt)
{ // Simulate operation of DFA on txt
int i, j, N = txt.length(), M = pat.length();
for (i = 0, j = 0; i<N && j<M; i++)
j = dfa[txt.charAt(i)][j];
if (j == M) return i-M; // Found
else return N; // Not found
}
/**
* Will print:
* % java KMP AACAA AABRAACADABRAACAADABRA
* text: AABRAACADABRAACAADABRA
* pattern: AACAA
*/
public static void main(String[] args)
{
String pat = args[0];
String txt = args[1];
KMP kmp = new KMP(pat);
StdOut.println("text: " + txt);
int offset = kmp.search(txt);
StdOut.print("pattern: ");
for (int i = 0; i < offset; i++)
StdOut.print(" ");
StdOut.println(pat);
}
}
Worst case processing time of KMP is N+M, since M time for preprocessing and N time for searching.
Boyer-Moore Substring Search
Boyer-Moore algorithm used heuristic method to find mismatched and scan each character in the direction right-to-left. Below the step by step of how Booyer-Moore algorithm doing mismatched character heuristic:
Let i = 0 and s = 0 for skip value.
Let j = length of pattern.
Compare character of pattern[j] with text[i+j].
If not matched, set s to j-(index of missmatched). then increment i by s. Back to step 2.
Else decrement j by 1 and back to step 3.
An image below illustrate how Boyer-Moore algorithm find pattern NEEDLE in the text FINDINAHAYSTACKNEEDLE.
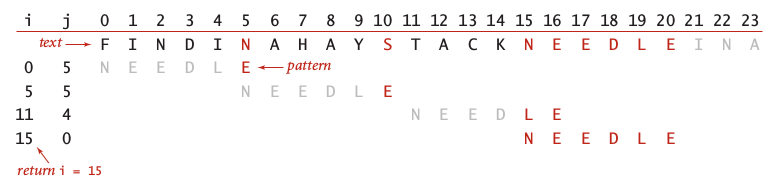
Image 10: Example of missmatched character heuristic
Obviously, we can do this in linear time by constructing an array to lookup which index in the pattern. Lets called that array as right[] since we used this array for reverse lookup, right to left. Simply, we just need to allocate R sized array, then filled each index by -1 for each index of character that not found in the pattern, and 0 to M for character found in the pattern by left order. The construction of right[] array for pattern NEEDLE illustrate in image 11.
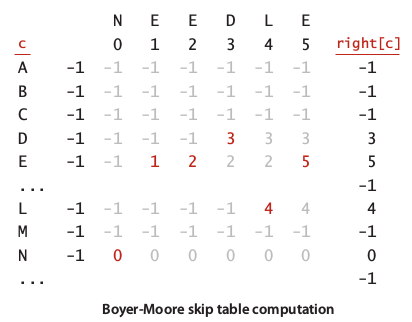
Image 11: Right array example
The implementation of Boyer-Moore algorithm in java will be like this:
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
class BoyerMoore
{
private int[] right;
private String pat;
BoyerMoore(String pat)
{ // Computer skip table
this.pat = pat;
int M = pat.length();
int R = 256;
right = new int[R];
for (int c=0; c<R; c++)
right[c] = -1;
for (int j=0; j<M; j++)
right[pat.charAt(j)] = j;
}
public int search(String txt)
{ // Search for pattern in txt
int N = txt.length();
int M = pat.length();
int skip;
for (int i=0; i<=N-M; i+=skip) {
skip = 0;
for (int j=M-1; j>=0; j--) {
if (pat.charAt(j) != txt.charAt(i+j)) {
skip = j-right[txt.charAt(i+j)];
if (skip<1) skip = 1;
break;
}
}
if (skip == 0) return i; // Found
}
return N; // Not found
}
/**
* Will print:
* % java BoyerMoore AACAA AABRAACADABRAACAADABRA
* text: AABRAACADABRAACAADABRA
* pattern: AACAA
*/
public static void main(String[] args)
{
String pat = args[0];
String txt = args[1];
BoyerMoore boyerMoore = new BoyerMoore(pat);
StdOut.println("text: " + txt);
int offset = boyerMoore.search(txt);
StdOut.print("pattern: ");
for (int i = 0; i < offset; i++)
StdOut.print(" ");
StdOut.println(pat);
}
}
The typical implementation of Boyer-Moore algorithm like code above will guarantee worst case running time to NM. Furthermore, a full implementation of Boyer-Moore will provide linear-time worst-case guarantee by implementing KMP-like table. If we look into Image 10, its like we can choose better skip value by implementing KMP-like array rather than simply decrement index of j.
Rabin-Karp Fingerprint Search
Rabin-Karp algorithm use hash function to encode pattern and substring of text, so a match occurred if only if encoded value of pattern equal to substring. We implement Horner method to do efficient modular hashing on substring of M length. A simple hash function of substring formulated by:
To avoid recalculation, we can derived formula above to compute next substring by subtracting one left most binomial value, increase the order of rest binomial and added a constant at last:
formula
To avoid exhaustive computation and reduce space (since length of integer 231), we only need to reproduce the remainder of each hash value. This method called as modular hashing.
formula
where Q is any prime number. This calculation is similar to calculation in hash table, but in this case, we do not store each hash value in a table, we only care of the hash value for each substring. Since choose for right value of Q is not trivial problem, we can guarantee that by choosing large enough value for Q, the probability of collision is 1/Q. This approach called as by Monte Carlo correctness. But, if in the case we use defensive approach, then we should ensure that matching always correct. In that case we used approach called as Las Vegas correctness. This approach required back-up for testing of correctness operation. Graphical implementation of Rabin-Karp algorithm illustrated in image below.
Image 12: Rabin-karp implementation
The implementation of Rabin-Karp algorithm in Java will be look like this:
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class RabinKarp
{
private String pat; // Only needed for Las Vegas
private long patHash;
private int M;
private long Q;
private int R = 256;
private long RM;
public RabinKarp(String pat)
{
this.pat = pat;
this.M = pat.length();
Q = longRandomPrime();
RM = 1;
for (int i = 1; i <= M; i++)
RM = (R * RM) % Q;
patHash = hash(pat, M);
}
// Monte carlo
// public boolean check(int i)
// {
// return true;
// }
// Las Vegas
public boolean check(String txt, int i)
{
for (int j = 0; j < M; j++)
if (pat.charAt(j) != txt.charAt(i+j))
return false;
return true;
}
private long hash(String key, int M)
{
long h = 0;
for (int j = 0; j < M; j++)
h = (R * h + key.charAt(j)) % Q;
return h;
}
private int search(String txt)
{
int N = txt.length();
long txtHash = hash(txt, M);
if (patHash == txtHash) return 0;
for (int i = M; i < N; i++) {
txtHash = (txtHash + Q - RM*txt.charAt(i-M) % Q) % Q;
txtHash = (txtHash*R + txt.charAt(i)) % Q;
int offset = i - M + 1;
if (patHash == txtHash && check(txt, offset))
return offset; // Match
}
return N; // No match found
}
}
Rabin-Karp substring search is known as fingerprint search because it uses a small amount of information to represent a pattern. Then it looks for this fingerprint (the hash value) in the text. The algorithm is efficient because the fingerprints can be efficiently computed and compared.